Text Analytics & Unsupervised NLP - Part II
In the first article of the Text Analytics & Unsupervised NLP series, I walked through importing your data, stop words, cleaning, and tokenizing and finished off with visualizing n-grams: uni-, bi- and tri-grams.
This article will focus on a few different applications of clustering. First, we’ll generate clusters of similar words across the corpus, then we’ll create a dendrogram to represent document-clusters based on topic, and finally we’ll do some topic modeling.
Load Data
Refer to the first article to load your data. This will pick up right where part I left off.
Word Clusters
Cluster words from the corpus into different groups.
Instead of using our tokenized lists of words, we’ll be using a TfidfVectorizer. In a nutshell, tfidf (term frequency-inverse document frequency) aims to find the most important words in a corpus. The rough calculation is below:
- Term frequency = frequency of word in document / total number of words in document
- Inverse document frequency = log_e(# of documents in corpus / number of documents with the particular word) TF-IDF = term frequency * inverse document frequency TF-IDF can be helpful, alongside a list of stop words, to determine the most important words. The more important the word, the higher the TF-IDF score. A low score would mean that the word appears frequently across all documents, which may signify that it’s unimportant and should be excluded from analysis.
So TF-IDF will help us build a vocabulary full of significant words (relatively speaking.) We’ll then use KMeans to cluster the words.
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.cluster import KMeans
from sklearn.metrics import adjusted_rand_score
documents = data['rawText'].tolist()
# max_df = cutoff score. words with higher scores are more rare
# min_df = cutoff score. words with lower score won't be included as they are too common
# max_features = # of top words to include within threshold
vectorizer = TfidfVectorizer(max_df=0.95, min_df=2, max_features=1000, stop_words='english')
X = vectorizer.
(documents)
n = 2 # number of clusters to make
model = KMeans(n_clusters=n, init='k-means++', max_iter=100, n_init=1,random_state=100)
model.fit(X)
print("Top terms per cluster:")
print('----------------------')
order_centroids = model.cluster_centers_.argsort()[:, ::-1]
terms = vectorizer.get_feature_names()
for i in range(n):
print("Cluster %d:" % i),
for ind in order_centroids[i, :10]:
print(' %s' % terms[ind])
print()
Top terms per cluster:
----------------------
Cluster 0:
trump
president
fox
mr
agency
house
abc
white
administration
tuesday
Cluster 1:
gun
people
says
students
food
new
mr
company
years
school
Now lets feed sentences into our KMeans model to predict which cluster it belongs in. The sentence will be vectorized with the TF-IDF vectorizer and then fed into the model.
sentence1 = "some people drink a lot of coffee"
sentence2 = "trump lives in the white house"
print("Prediction")
Y = vectorizer.transform([sentence1])
prediction = model.predict(Y)
print(sentence1,'belongs in: cluster', prediction[0])
Y = vectorizer.transform([sentence2])
prediction = model.predict(Y)
print(sentence2,'belongs in: cluster', prediction[0])
Prediction
some people drink a lot of coffee belongs in: cluster 1
trump lives in the white house belongs in: cluster 0
Pretty cool!
Document Clustering (based on topic)
With a large collection of documents, it might be hard to figure out where to start. A team recently came to me and asked what I could do for them, and the following gave them a great jumping off point. Clustering documents together by topic allowed them to divvy out documents to their team of research in an efficient manner, and visually represented by a dendrogram.
The following function uses our TD-IDF vectorizer, and then calculates cosine similarity to try and find documents with a similar score. The closer the score, the more similar the docuemnts probably are. We’ll then use ward clustering, where we metaphorically start out at the leaves and work our way in to the branches of the tree. The ward clustering uses our calculated cosine similarity scores, and will group documents with the similar scores.
from scipy.cluster.hierarchy import ward, dendrogram
from matplotlib import pyplot as plt
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
def view_doc_tree(data,save_as=False):
# get a list of the raw text from each article
synopses = data['rawText'].tolist()
# create a TF-IDF vectorizer:
tfidf_vectorizer = TfidfVectorizer(#max_df=0.9,
max_features=200000,
#min_df=0.1,
stop_words='english', random_state=10,
use_idf=True, ngram_range=(1,4))
# calculate TF-IDF
# this gives a weight to words based on their frequency in a document and the inverse frequency across all documents
# idea: words that are frequent in a document, but also very frequent in other documents, might just be noisy
# idea: words that are frequent in a document, and infrequent across other docuemnts, can help determine the article's topic
tfidf_matrix = tfidf_vectorizer.fit_transform(synopses) #fit the vectorizer to synopses
terms = tfidf_vectorizer.get_feature_names()
# now calculate the tf-idf cosine difference
# this helps us cluster documents that might be similar
dist = 1 - cosine_similarity(tfidf_matrix)
# use ward clustering to find similar docs;
# cluster analysis as an analysis of variance problem instead of using distance metrics or measures of association
# agglomerative clustering algorithm: start out at the leaves and work its way to the trunk, so to speak.
# It looks for groups of leaves that it forms into branches, the branches into limbs and eventually into the trunk.
linkage_matrix = ward(dist) #define the linkage_matrix using ward clustering pre-computed distances
titles = data['filename'].tolist()
fig, ax = plt.subplots(figsize=(15, 20)) # set size
# visualize the linkage matrix with a dendogram
ax = dendrogram(linkage_matrix, orientation="right", labels=titles);
plt.tick_params(\
axis= 'x', # changes apply to the x-axis
which='both', # both major and minor ticks are affected
bottom='off', # ticks along the bottom edge are off
top='off', # ticks along the top edge are off
labelbottom='off')
plt.tight_layout() #show plot with tight layout
if save_as:
plt.savefig(save_as, dpi=200) #save figure as ward_clusters
plt.show()
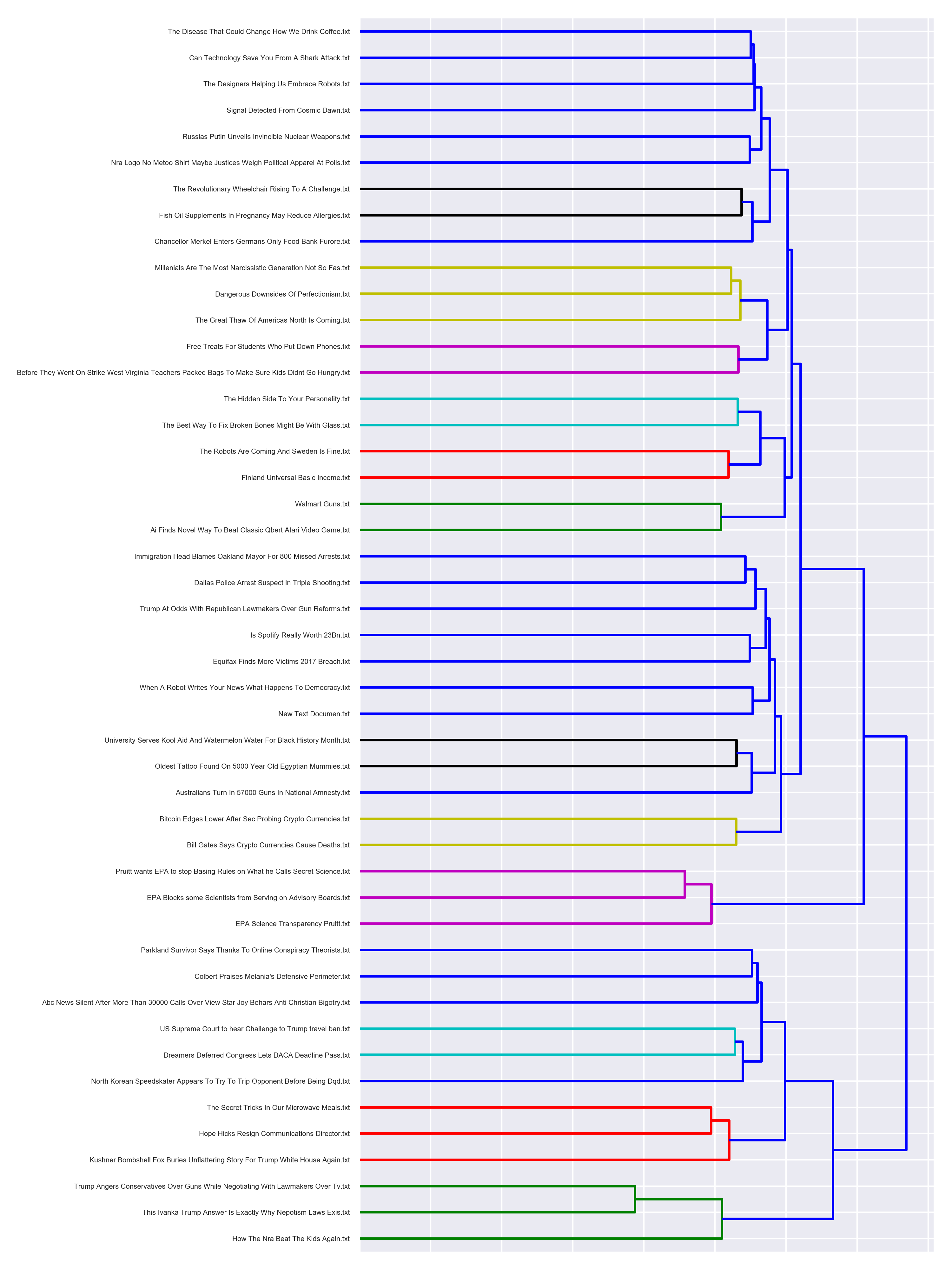
It’s far from perfect, but it’s also pretty interesting to see how good some of the connections are, based on article headlines alone. Change the parameters in the TF-IDF vectorizer to see how setting the max_df, min_df can totally change the outcome. The initial state of the function ignores those preferences.
Topic Modeling
We have already fit a TF-IDF vectorizer above, set to X, and will recycle this to do topic modeling. First, we’ll use these scores as a threshold to try and cut down the number/quality of words that we want to work with.
vocab = vectorizer.vocabulary_
idf = vectorizer.idf_
vocab
{'abil': 0,
'absorb': 1,
'accept': 2,
'access': 3,
'accumul': 4,
'accus': 5,
'achiev': 6,
'action': 7,
'activ': 8,
'ad': 9,
'add': 10,
'address': 11,
'administr': 12,
'admit': 13,
'advanc': 14,
'advertis': 15,
'advis': 16,
'affect': 17,
'afternoon': 18,
'age': 19,
'agenc': 20,
'ago': 21,
'agre': 22,
'agreement': 23,
'aid': 24,
'aim': 25,
'air': 26,
'alleg': 27,
'allow': 28,
'america': 29,
'american': 30,
'amount': 31,
'announc': 32,
'answer': 33,
'appear': 34,
'approach': 35,
'area': 36,
'argu': 37,
'arm': 38,
'arriv': 39,
'artifici': 40,
'ask': 41,
'aspect': 42,
'assess': 43,
'associ': 44,
'attack': 45,
'attempt': 46,
'audienc': 47,
'author': 48,
'averag': 49,
'avoid': 50,
'background': 51,
'bad': 52,
'ban': 53,
'base': 54,
'basic': 55,
'bear': 56,
'began': 57,
'believ': 58,
'benefit': 59,
'best': 60,
'better': 61,
'big': 62,
'biggest': 63,
'bill': 64,
'billion': 65,
'board': 66,
'bodi': 67,
'book': 68,
'break': 69,
'bring': 70,
'british': 71,
'broadcast': 72,
'build': 73,
'busi': 74,
'buy': 75,
'call': 76,
'campaign': 77,
'care': 78,
...
The list above represents the words in the entire vocabulary. As you’ll see, some have pretty low frequencies. Let’s keep words that have an idf score (Inverse-document frequency) over the 50th percentile.
# keep only the words with idf score above the 50th percentile
# need words that are pretty unique/rare to help us figure out what
vocab_keep = np.where(idf >= np.percentile(idf, 50))[0]
vocab = [k for k,v in vocab.items() if v in vocab_keep]
print('{} words in the vocabulary'.format(len(vocab)))
315 words in the vocabulary
Now onto the actual topic modeling. We’ll be running an LDA model (Latent Dirichlet Allocation) which tries to find the connections between words and an identified number of topics. This number can be set within LdaModel(num_topics=?).
from gensim import corpora, models
texts = [[token for token in tokens.split() if token in vocab] for tokens in data.tokens_stem]
id2word = corpora.Dictionary(texts)
corpus = [id2word.doc2bow(text) for text in texts]
model = models.ldamodel.LdaModel(corpus, num_topics=5, id2word=id2word, random_state=1)
model.print_topics(num_topics=5, num_words=5)
Topic modeling, if you haven’t done it before, doesn’t exactly give you solid topics. There’s a lot of reading in-between the lines that needs to be done in order to come up with the actual topic that a bunch of words represent. See the results below:
[(0,
'0.028*"gun" + 0.017*"olymp" + 0.016*"accus" + 0.013*"sport" + 0.013*"advis"'),
(1,
'0.040*"devic" + 0.020*"score" + 0.016*"attack" + 0.011*"highli" + 0.011*"member"'),
(2,
'0.022*"food" + 0.020*"gun" + 0.011*"polic" + 0.011*"teacher" + 0.010*"west"'),
(3,
'0.041*"robot" + 0.038*"design" + 0.022*"food" + 0.016*"water" + 0.014*"climat"'),
(4,
'0.027*"robot" + 0.024*"justic" + 0.022*"gun" + 0.019*"basic" + 0.014*"immigr"')]
Finally, let’s visualize our LDA model. pyLDAvis provides an awesome interactive tool that lets you explore the topics. Play around with lambda at the top right corner–a lower value tends to get you terms within a topic that are more descriptive of the particular topic, so the relevance to other topics is lower. Play around with this and then continue on to part III of this text analytics, unsupervised NLP series where I’ll do a quick demonstration of random sentence generation.
import pyLDAvis.gensim
reviews_vis = pyLDAvis.gensim.prepare(model, corpus, id2word)
pyLDAvis.display(reviews_vis)